Modelo Black-Scholes

Para comenzar, Fisher Black y Myron Scholes son los autores del modelo Black and Scholes. Ellos dieron a conocer su ecuación a través de la revista Journal of Political Economy en el año 1973. El objetivo de la ecuación es determinar el precio de no arbitraje que un inversionista debe pagar por el derecho a la compra-venta de activos financieros, siempre que sea en un tiempo previamente pactado y establecido.

Por lo que se refiere a Trade Off, sabe lo importante que es para usted el crecimiento de su empresa. Por esta razón, pone a su disposición la aplicación de la ingeniería financiera para su negocio, con el fin de, brindarle instrumentos financieros que permitan la reestructuración de sus finanzas y mejorar el perfil de sus inversiones.

Contextualizando el modelo Black and Scholes

Actualmente, en el mercado hay una gran variedad de productos financieros, no obstante, los derivados y sus combinaciones son los más utilizados, como: las opciones, los forwards y los swaps. Dentro del mercado de opciones, los derivados son los que mayor avance financiero y tecnológico han alcanzado. Es así que, el modelo logró un gran impulso y a través de sus razonamientos matemáticos se posicionó como la mejor solución de valuación de opciones hasta el momento.

Para comprender mejor el mercado de opciones, se define una opción como un producto derivado con la particularidad de materializarse en un contrato que otorga al titular el derecho, pero no la obligación, de:

• Comprar (call)
• o de vender (put)
• el activo subyacente (S) a un
• precio de ejercicio predeterminado o strike (K)
• en una fecha determinada (T),
• considerando que las opciones requieren un pago inicial o prima (V en general, P para put y C para call), por lo que tienen un costo inicial. Bernardo, (2014).

Dado que, las opciones otorgan un derecho y no una obligación, se consideran tres opciones en las que pueden encontrarse:

• “In the money”: hacen referencia a las opciones que si se ejercen otorgan beneficios a su titular.
• “Out of the money”: se refiere a la posición en las que no se ejercen, porque traerían pérdidas al titular.
• “At the money”: posición en la que no se generan pérdidas, pero tampoco beneficios si se ejercen.

¿Cómo funciona la ecuación de Black and Scholes?

A su vez, ambos autores modelan el precio del activo subyacente (evolución del precio de otros activos), como un proceso estocástico, mediante un movimiento browniano geométrico (desplazamiento aleatorio que se observa en algunas partículas microscópicas cuando se encuentran en un medio fluido). Además, incluyen los efectos provocados por el precio y la volatilidad. En este sentido, cabe mencionar que, es a partir del lema de Itô que obtienen dicha ecuación, de carácter estocástica diferencial que les permitió determinar el valor de la opción financiera. Sin embargo, para que este modelo resulte, la clave está en que, por medio de una operación de cobertura de riesgo, se consiga reducir esta ecuación a una diferencial clásica.

Con respecto al precio de una opción, la fecha de su expiración coincide con su payoff, puesto que, en ese momento desaparece la incertidumbre que existía hasta antes de que ocurriera la expiración. Entonces, lo que Black and Scholes buscaban era determinar mediante una ecuación el precio justo de una opción antes del momento de su expiración. Correspondiendo así, con la hipótesis de mercado eficientes, la cual manifiesta que: el mercado responde de manera instantánea a la nueva información disponible, por consiguiente, el precio actual solo va a depender del precio pasado más reciente.

En consecuencia, obtuvieron una ecuación diferencial clásica sin la parte estocástica que les permitió determinar tanto el comportamiento de una opción de tipo call, como put, resolviendo así, el problema.

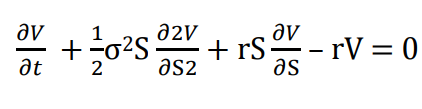
Cálculo de Itô

Por otra parte, el cálculo de Itô permite extender los métodos del cálculo a procesos estocásticos. Una de las características principales es que tiene aplicaciones muy importantes en matemáticas financieras y en ecuaciones diferenciales estocásticas. Por consiguiente, en el mercado de acciones, los operadores emplean este análisis para saber en qué momento les conviene comprar o vender títulos. Dado que, hace referencia a las oscilaciones que existen en los precios de cierre. Desde este punto de vista, el cálculo de Itô se utiliza para derivar el proceso estocástico seguido por el precio de un título derivado.

Por último, la relación entre este cálculo y el principio browniano es que: “si dos valores tienen la misma fuente de riesgo, una combinación apropiada de los dos valores puede eliminar ese riesgo; dicho de esta manera, los derivados financieros nacieron para limitar dichos riesgos”. Gil, (2015).

Por todo esto, Trade Off le invita a contactar con nosotros, con la intención de aplicar la ingeniería financiera a su negocio. E igualmente, le proporciona: claridad en su modelo financiero, eficacia en su operación comercial, visión del crecimiento de su negocio e información que le permitirá aprovechar oportunidades de negocios únicas.

Envíe un mensaje y conozca los beneficios y directrices de esta ingeniería y las garantías que tenemos para usted.  

Fuentes consultadas

• Universidad de Salamanca, Bernardo, 2014, “Valoración de opciones. Modelo europeo. Aproximación numérica.”
• Villamil, 2006, Modelos de valoración de opciones europeas en tiempo continuo.
• UAEH, Duana & Millán, “Modelo Black-Scholes-Merton, para la toma de decisiones financieras”
• Economipedia, 2015, Gil, Lema de Ito